二等辺三角形になるための条件(1) 二等辺三角形になるための条件 定理 三角形の2つの角が等しければ、その三角形は等しい2つの角を底角 とする二等辺三角形である。 1 下の図のように、AB=ACの二等辺三角形ABCの辺AB,AC上にそれぞれ各辺の比が決まった三角形がある 三角形の中でも、各辺の比率が決まっている三角形が存在します。 これらの三角形は、図形を学習していく上で特に重要なので、この機会に覚えてしまいましょう。 直角と45°の組合せ まず、次の図のような直角二等辺三角形です 斜辺が4cmの直角二等辺三角形DEFがいたとしよう。 こいつの斜辺以外の長さは公式をつかうと、 EF = √2/2 × 4 = 2√2 cm になるよ! 分数の計算だからミスをしないように気をつけてね^^ まとめ:直角二等辺三角形の辺の長さの求め方は2通りでクリア!
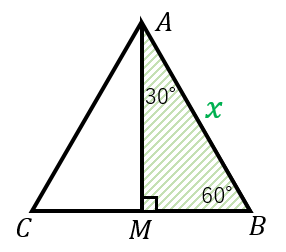
30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学
直角二等辺三角形 比
直角二等辺三角形 比-そして試験官も面倒くさいということで、 数値がキレイに出てくる三角比が問題にはよく出されます。 それは 角度が30°、60°、90°の直角三角形 と、 角度が45°、45°、90°の直角二等辺三角左の直角三角形は、正三角形を半分にしたものです。 \(3\) 辺の比は暗記で、\(21\sqrt{3}\) です。 よって、下の図のように長さが決まります。 \(x=3\sqrt{3}\) です。 右の直角三角形は、正方形を半分にした直角二等辺三角形です。
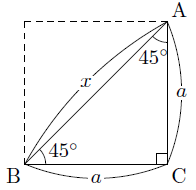



三角定規の3辺の比 まなびの学園
ここでは,よく使われる特別な直角三角形の辺の比について学習してみましょう。 特別な直角三角形 ① 直角二等辺三角形 ② 30 °,60 °,90 °の直角三角形 11 2:: 132:: ③ 整数比の辺をもつ直角三角形 345:: ::三角定規になっている直角二等辺三角形と、正三角形を半分にした三角形は角度がそれぞれ 45°, 45°, 90° と 30°, 60°, 90°となり、3辺の長さの比が次のようになる。 特別な直角三角形の3辺の比 45° 45° 1 1 2 60° 30° 1 2 3基本的な三角形と三角比 正方形の半分 直角二等辺三角形(各辺の比は 1 1 2) sin 45 ° = BC AB = 1 2 cos 45 ° = AC AB = 1 2 tan 45 ° = BC AC = 1 1 正三角形の半分 各辺の比が 1 2 3 の直角三角形 sin 30 ° = BC AB = 1 2 cos 30 ° = AC AB = 3 2 tan 30 ° = BC AC = 1 3 sin 60 ° = AC AB = 3 2 cos 60 ° = BC AB = 1 2 tan 60 ° = AC BC = 3 1
直角二等辺三角形だと この公式。 と別々に覚えるのは大変ですね。 ですので、やみくもに公式を覚えるのではなく、 (底辺) × (高さ) ÷ 2 が当てはまる、 底辺 と 高さ を探す ほうが、簡単 だと思います。 三角形の面積公式が (底辺) × (高さ) ÷ 2 となる三角定規には、\(\boldsymbol{45^{\circ}}\) の角を持つ直角二等辺三角形と、\(\boldsymbol{30^{\circ},\;60^{\circ}}\) の角を持つ直角三角形の \(2\) 種類があり、それぞれ 特別な \(\boldsymbol{3}\) 辺の長さの比 を持ちます。直角二等辺三角形の選択入力値から他の要素の値を計算します。 h = a 2 b = a √ 2 L = ( 1 √ 2 ) a S = a 2 4 h = a 2 b = a 2 L = ( 1 2 ) a S = a 2 4 入力指定
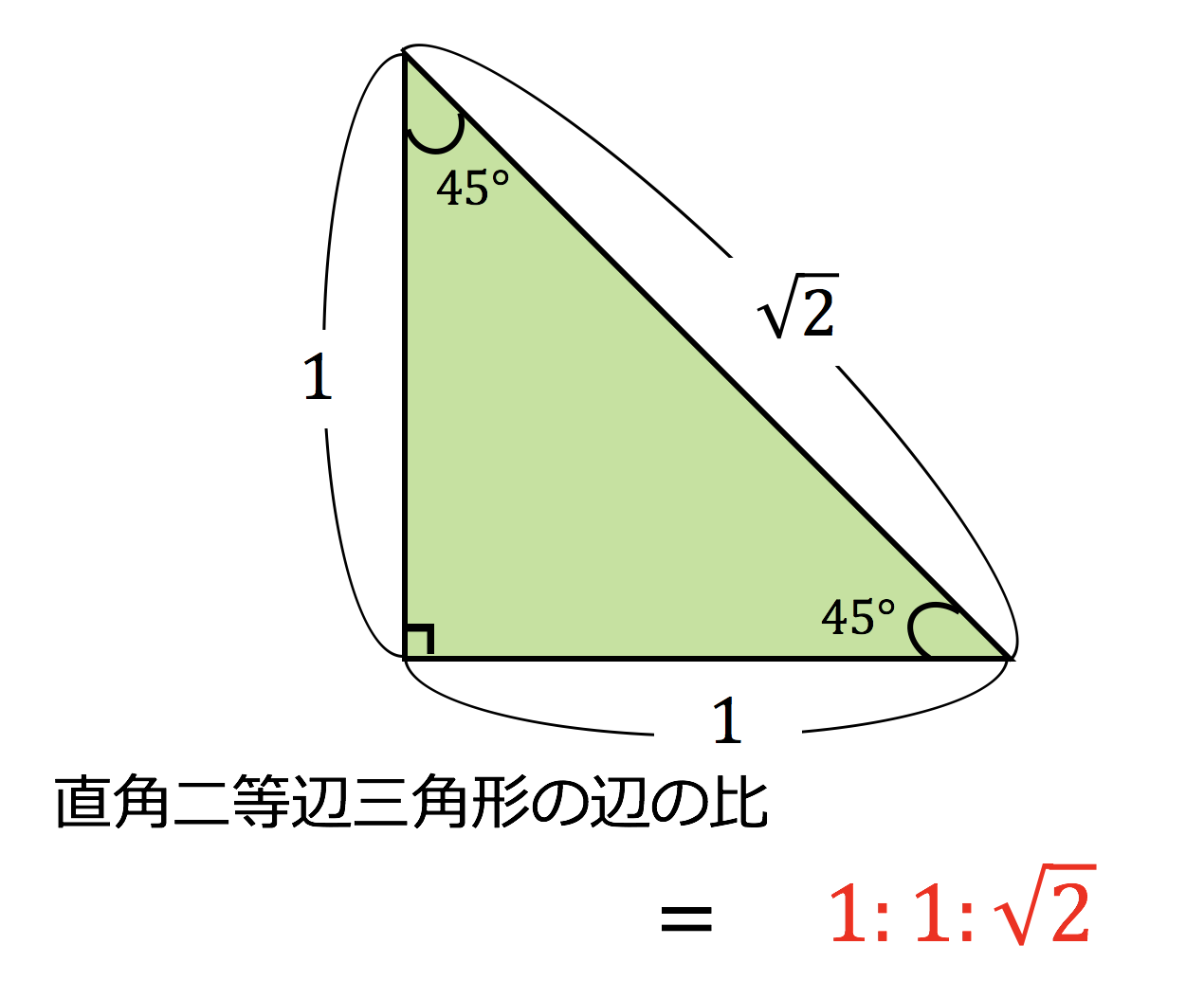
直角三角形は面積 ab の長方形を1本の対角線で区切って2等分した図形なので、面積は ab/2 である。また、合同な2つの直角三角形を、直角の頂点同士および他のもう1角の頂点同士が重なるように並べると二等辺三角形ができる。直角三角形は直角に対する辺がいちばん長くなります。 正三角形です。 すべての辺の長さは同じ です。 辺の長さの比1:1:1 直角二等辺三角形です。 直角をはさむ2辺の長さは同じ です。 辺の長さの比1:1:√2 60°と30°の直角三角形です。 いちばん長い辺はいちばん短い辺の2倍の長さ です直角二等辺三角形の定規の辺の比は、11 √2(内角は、90°、45°、45°) この場合、斜辺が√2です。 1² + 1² =√2² また、直角二等辺三角形といえば、正方形を対角線で半分に切った図形です。



二等辺三角形の底辺は 1分でわかる意味 長さの計算 角度 高さ 三平方の定理との関係




頂角36度の二等辺三角形の辺の比を教えてください 頂角36度の二等辺三 数学 教えて Goo
直角二等辺三角形なら、 どこか \(1\) 辺の長ささえわかれば、自動的に残りの辺の長さもわかる ということを覚えておいてくださいね。 補足 「直角二等辺三角形」については、以下の記事も参考にしてみてください。直角二等辺三角形(ちょっかくにとうへんさんかくけい、英 isosceles right triangle )は、二等辺三角形の持つ特徴に加え、直角三角形の持つ特徴を併せ持つ図形である。 3つの角のうち2つの角がそれぞれ45°である三角形と定義してもよい。 直角二等辺三角形は二等辺三角形の一つでもあり、直角1つの三角形において 6 三角形の合同条件 ①3辺相等 ②2辺夾角相等 ③2角夾辺相等 7 直角三角形の合同条件 ①斜辺と1つの鋭角がそれぞれ等しい ②斜辺と他の1辺がそれぞれ等しい 8 二等辺三角形の性質 ①両底角が等しい ②頂点の二等分線と底角の垂直二等



直角二等辺三角形befの面積は 2006年算数オリンピック ファイナル問題より 算数オリンピック問題に挑戦
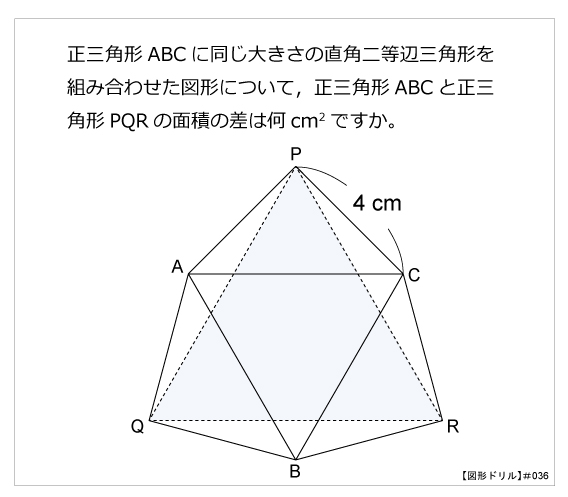



直角二等辺三角形 算数星人のweb問題集 中学受験算数の問題に挑戦
直角二等辺三角形の辺の長さの比は1:1: 2 でしたね。 したがって,x:6 = 1: 2 から 2 x = 6 を解いて 66× 26 2 = = = = 3 2 直角二等辺三角形の辺の比は、必ず「\(\color{red}{1 1 \sqrt{2}}\)」 となります。 \(1\) 辺の長さからほかの辺の長さを簡単に求められるので、この比は必ず覚えておきましょう。Sin B = b c {\displaystyle \sin B= {\frac {b} {c}}} cos B = a c {\displaystyle \cos B= {\frac {a} {c}}} tan B = b a {\displaystyle \tan B= {\frac {b} {a}}} と表す。 なお sin 2 B cos 2 B = b 2 a 2 c 2 = 1 {\displaystyle \sin ^ {2}B\cos ^ {2}B= {\frac {b^ {2}a^ {2}} {c^ {2}}}=1} である。




30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ
直角二等辺三角形の底辺と高さの長さは同じです。 底辺(高さ)の長さを「1」として、三平方の定理に代入すると「斜辺 2 =底辺 2 高さ 2 ⇒ 斜辺 2 =11=2 ⇒ 斜辺=√2」になります。 よって、直角二等辺三角形の辺の比は「1:1;√2」です。 直角二等辺三角形 直角(90度)以外の二つの角度は45度 。 正三角形と直角三角形 正三角形はすべての角度が60°。 正三角形を半分にすると「30°、60°、90°の直角三角形」になり、 一番長い辺が一番短い辺の2倍の長さになる 。 三角形の面積の公式―底辺× 辺の比率 直角三角形の性質を有することから、その辺の比に三平方の定理を適用することができ、結果として、その辺の比にかなりの特殊性が生まれることになります。 つまり、内角がそれぞれ90°、45°、45°の二等辺三角形の三辺の比は、1:1:√2となるのです。 この公式はかなりの頻度で利用する必要が生まれますので、是非とも覚えてしまうことをお
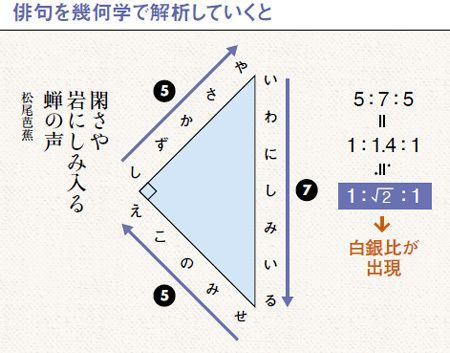



5 7 5 の俳句に隠されていた 白銀比 2ページ目 President Online プレジデントオンライン




中学数学 三平方の定理 直角二等辺三角形 オンライン無料塾 ターンナップ Youtube
次の直角三角形の辺の比は、 1 1 √2 だよ。 これは直角三角形の角度がそれぞれ、 45° 45° 90° の奴なんだ。 内角のうちの2つの角度が等しいから、 直角二等辺三角形 ってわけね。 辺の比を使ってやると、三平方の定理を使わずに辺の長さ出せるよ。 まぁ、三平方の定理でも解けますね。 しかし、もし、4ではなく04などの小数や分数が出た場合は、ちょっと計算が苦しくなります。 あくまでも、一時しのぎと考えて使ってください。 本来は、 比を利用するのがベスト です。 Tweet ← 受験数学:三平方105 ∘ = 90 ∘ 15 ∘ であるから、 90 ∘ θ の三角比より次のように求めることができる。 sin 105 ∘ = sin ( 90 ∘ 15 ∘) = cos 15 ∘ = √ 6 √ 2 4 cos 105 ∘ = cos ( 90 ∘ 15 ∘) = − sin 15 ∘ = − √ 6 − √ 2 4 tan 105 ∘ = tan ( 90 ∘ 15 ∘) = − 1 tan 15 ∘ = − 2 − √ 3 165 ∘ = 180 ∘ − 15 ∘ であるから、 180 ∘ − θ の三角比より次のように求めることができる。
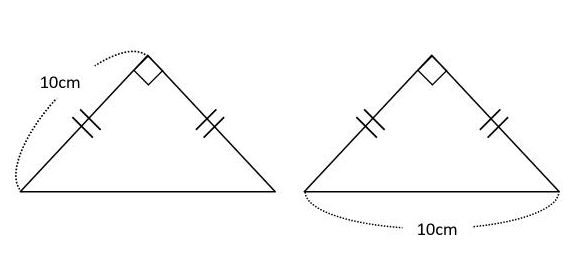



二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ
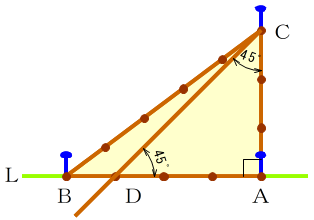



3 4 5の三角形で 本当に直角ができる Note Board
この問題に答えるためには,辺の比が1: で,その間の角度が45°のときは,「1:1: の直角二等辺三角形になる」という中学校数学の基本が前もって分かっていなければなりません. このことに気づかない場合は, などと,ab間の距離も求める必要があります.直角三角形(2本のバー、2a の棒と、中点から a の棒の例のフレーム)を2組、3つのノードの内各2つ同士はつなぎ、Z 軸方向にし、立体に組み、同じ可変長高さにする。xy 平面には2等辺三角形ができる。共通 Z 軸の足が、2等辺三角形の頂点となる。三角比 とは、直角三角形の3つある角の90度以外のどちらか1つの角度が決まれば、3つの辺の長さの比率が決まるという性質のことです。 注意:直角二等辺三角形の場合は角度が決まらなくても3辺の比率は決まってしまいます。 三角比として頻繁にでてくる角度は、 30度と45度と60度 です。 中学生では、この3つの角度の時の三角形の比率を全て覚えておけば、数学の




直角二等辺三角形の辺の求め方 直角二等辺三角形の底辺が106センチメ 数学 教えて Goo
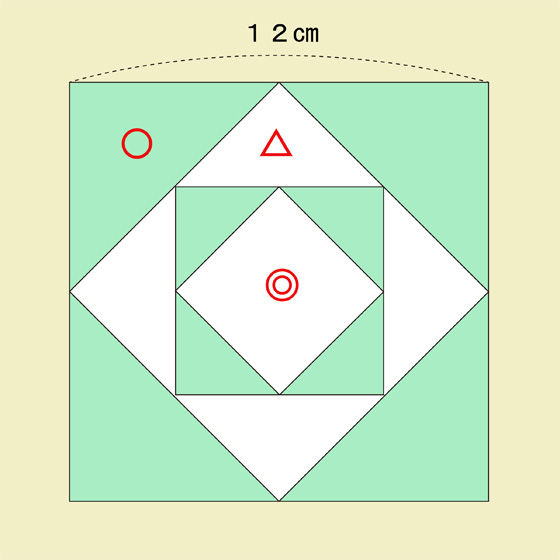



簡単に答えを出す方法に気付けるか 白い部分の面積を求める問題 秒刊sunday
数学中271 直角三角形の合同条件 Duration 数学中264 二等辺三角形 数学検定対策講座 準二級 三角比の相互関係1ベクトルの平行条件,垂直条件 3点が一直線上にある条件 → 携帯版は別頁 == 三角形の重心,内心,外心,垂心 (ベクトル,三角関数) == このページで解説する内容 各々その項目をクリックすれば解説にジャンプします 原点を O とし, ABC の頂点の位置第269問 直角三角形の特徴 図形ドリル 6年生 直角三角形 直角二等辺三角形 辺の比 面積比 ★★★★☆☆(中学入試難関校レベル) 思わず「お~~! ! 」と言いそうな良問を。 受験算数の定番からマニアックな問題まで。 図形ドリルでは,色々な




證明 15 75 90邊比與三角函數 Youtube
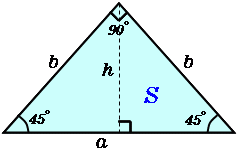



直角二等辺三角形 高精度計算サイト
二つの特別な直角三角形の角度と辺の長さの比の関係を暗記しよう! 「サイト内お気に入り」に登録する 数多の直角三角形のうち、二つの特別な直角三角形の三つの辺「底辺」「高さ」「斜辺」の長さの比の関係は簡単な数字で表される。 二つの特別な直角二等辺三角形 (ちょっかくにとうへんさんかくけい、 英 isosceles right triangle )は、 二等辺三角形 の持つ特徴に加え、 直角三角形 の持つ特徴を併せ持つ 図形 である。 3つの 角 のうち2つの角がそれぞれ45°である三角形と定義してもよい。第3章 三角比 − ポイント1 有名な角度の、sinθ、cosθ、tanθを知る 三角定規の三角形 (直角二等辺三角形) (正三角形
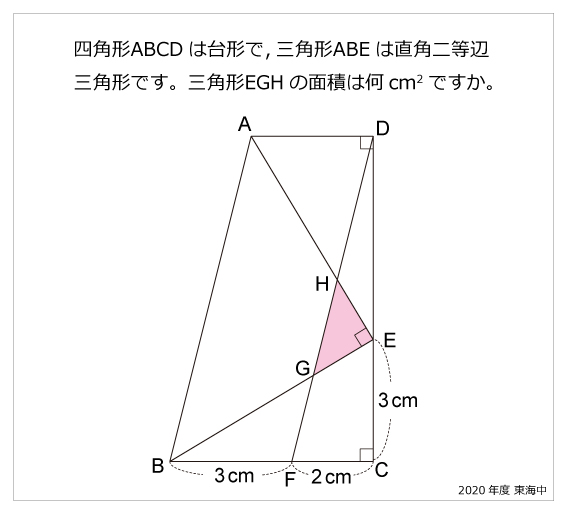



直角二等辺三角形 算数星人のweb問題集 中学受験算数の問題に挑戦



直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典
}{ 11\sqrt{ 2 } }\)になります。 この辺の比を覚えておくことで、底辺から斜辺の長さを求めたり、またその逆のことができます。二等辺三角形(二つの合同な辺を持つ三角形)において、合同でない辺を底辺として持つ頂垂線は、その辺の中点を足に持つ。 また合同でない辺を底辺とする頂垂線は、その頂角の二等分線である。 頂垂線またはその長さを表すのにしばしば文字 h (height に由来) が用いられ、対応する頂点を 今、二等辺三角形が熱い! ~小学校の算数が懐かしい デイリーポータルZ 21年5月31日 自分が小学生時代に流行ったマンガやアニメ、おもちゃなどに触れると、懐かしむのみならず改めてハマってしまうことはないだろうか。 筆者は最近、で中学




0405 直角三角形內最大的正方形面積 Youtube




簡単公式 直角二等辺三角形の辺の長さの2つの求め方 Qikeru 学びを楽しくわかりやすく
第233問 直角二等辺の辺の比 図形ドリル 直角三角形 直角二等辺三角形 相似 ★★★★★☆(算オリ・灘中受験生レベル) 思わず「お~~! ! 」と言いそうな良問を。 受験算数の定番からマニアックな問題まで。 図形ドリルでは,色々なタイプの



直角二等辺三角形とは 定義や辺の長さの比 面積の求め方 受験辞典




三角定規の3辺の比 まなびの学園
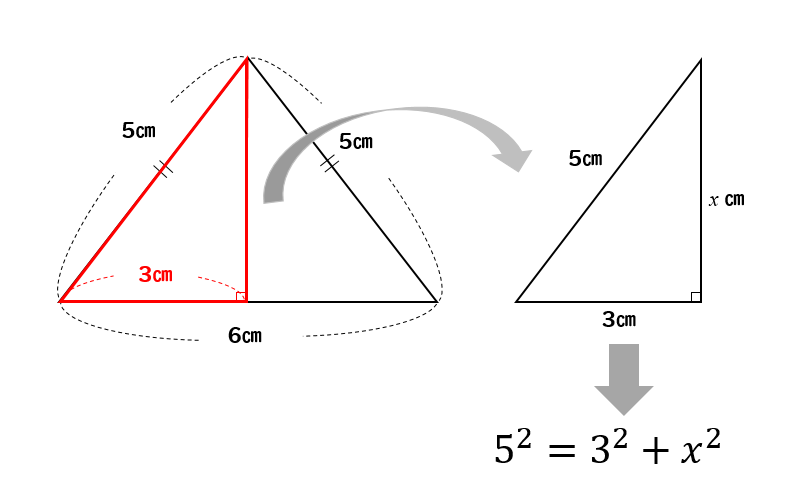



高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ



直角二等辺三角形とは 定義や辺の長さの比 面積の求め方 受験辞典



数学の質問です ルート2はどこから分かるんですか 直角二等辺三角 Yahoo 知恵袋




よく使う三角比の値 数学i By Okボーイ マナペディア




直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学




直角二等辺三角形の第三の頂点 香料ゐっすゐの夢



直角二等辺三角形とは 定義や辺の長さの比 面積の求め方 受験辞典



直角二等辺三角形とは 定義や辺の長さの比 面積の求め方 受験辞典



直角二等辺三角形とは 定義や辺の長さの比 面積の求め方 受験辞典




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ



直角二等辺三角形と三平方の定理の関係は 3分でわかる計算 公式 辺の比 例題
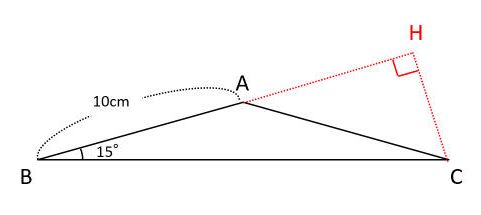



二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ



高校入試 英語 数学 特別な直角三角形
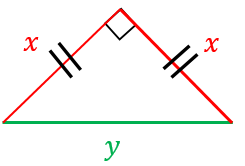



直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学




簡単公式 直角二等辺三角形の辺の長さの2つの求め方 Qikeru 学びを楽しくわかりやすく
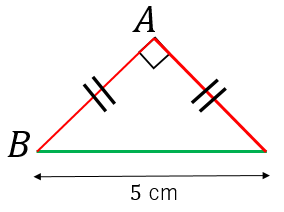



直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学
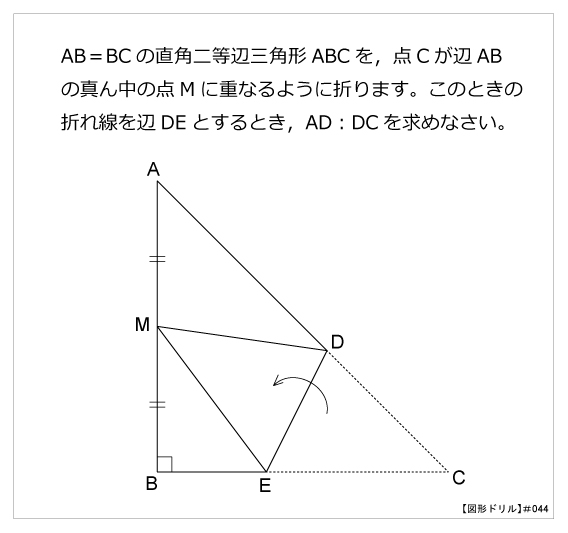



図形ドリル 第44問 直角二等辺三角形を折り返す 算数星人のweb問題集 中学受験算数の問題に挑戦



三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典




3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ




直角2等辺三角形と平行線 幾何学の証明がわからないので質問します 直 Okwave




各辺の比が決まっている三角形 中学数学 By Okボーイ マナペディア




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ
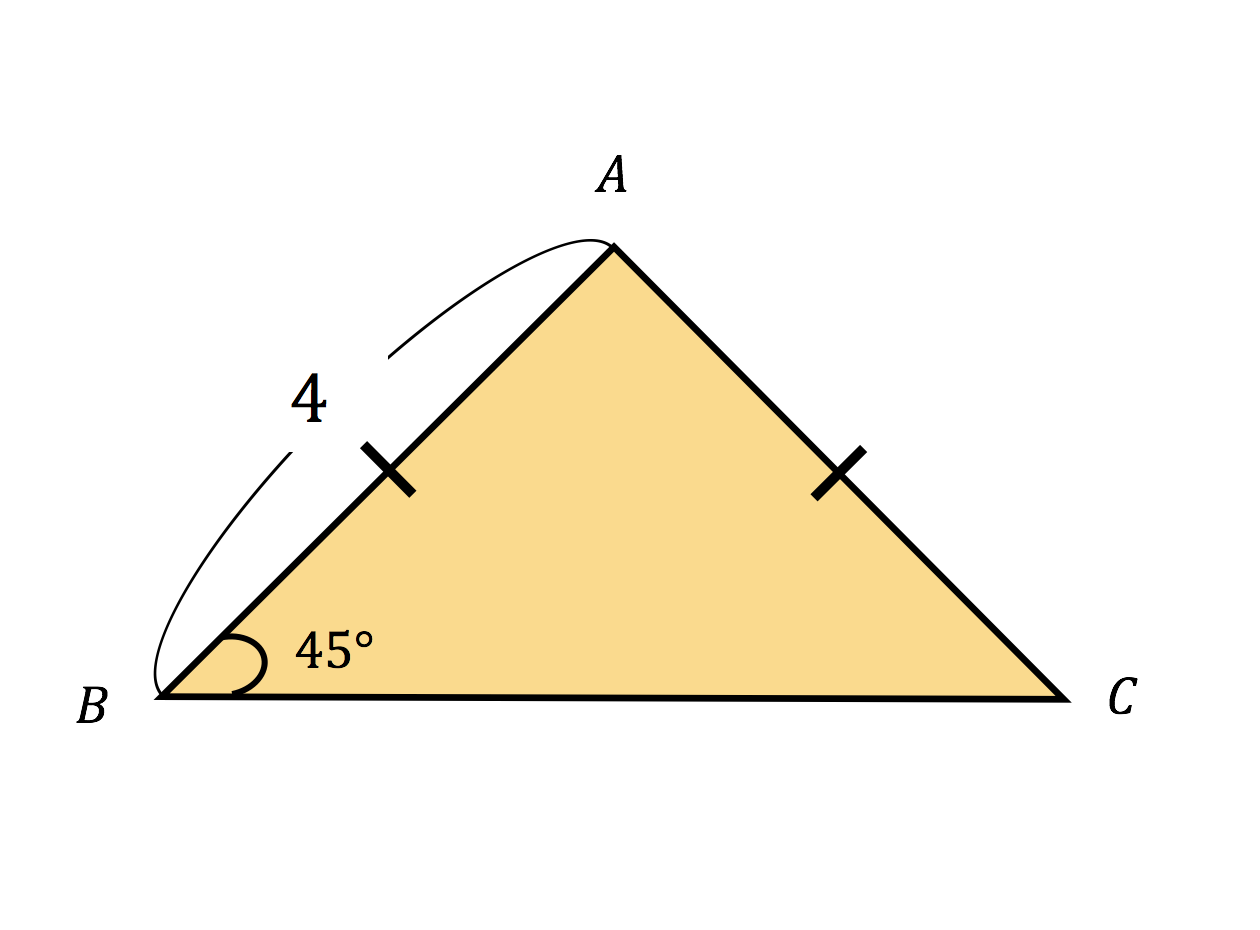



3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ
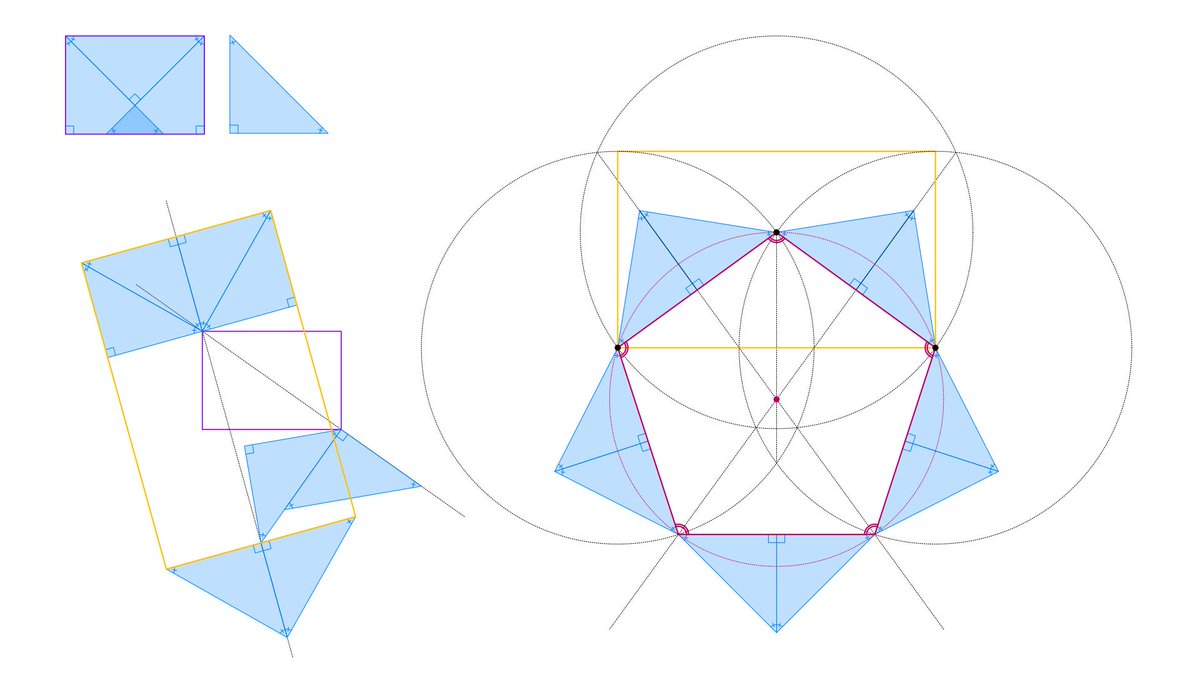



白銀長方形




テストによく出る直角三角形の辺の比 中学数学 By じょばんに マナペディア



直角二等辺三角形とは 定義や辺の長さの比 面積の求め方 受験辞典
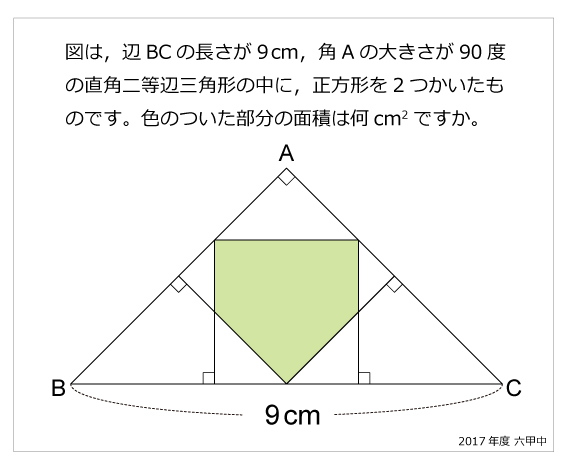



直角二等辺三角形 算数星人のweb問題集 中学受験算数の問題に挑戦




なぜ三角形cdeは直角二等辺三角形だとわかるのかが理解できません 教えてください Clear
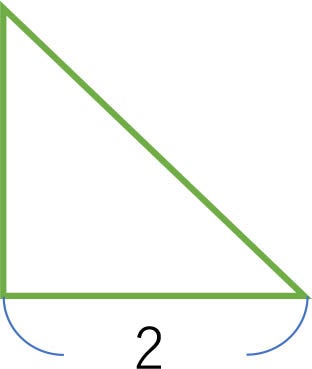



面積 直角二等辺三角形 小学4年生算数 そらいろ日記 言葉の宝箱




簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




簡単公式 直角二等辺三角形の辺の長さの2つの求め方 Qikeru 学びを楽しくわかりやすく




数学の内心の問題です 1 1 2の比の直角三角形の内接円の半径が1セン 数学 教えて Goo




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ
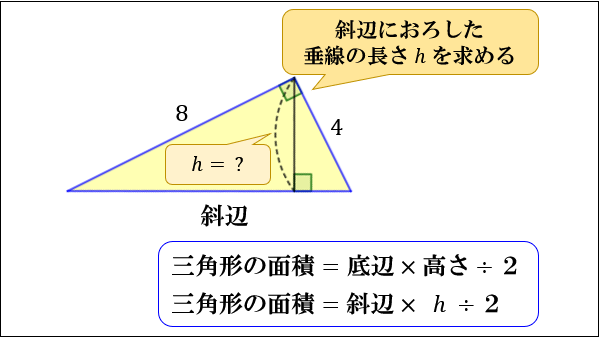



トップ100 正三角形面積小学生 最高のカラーリングのアイデア
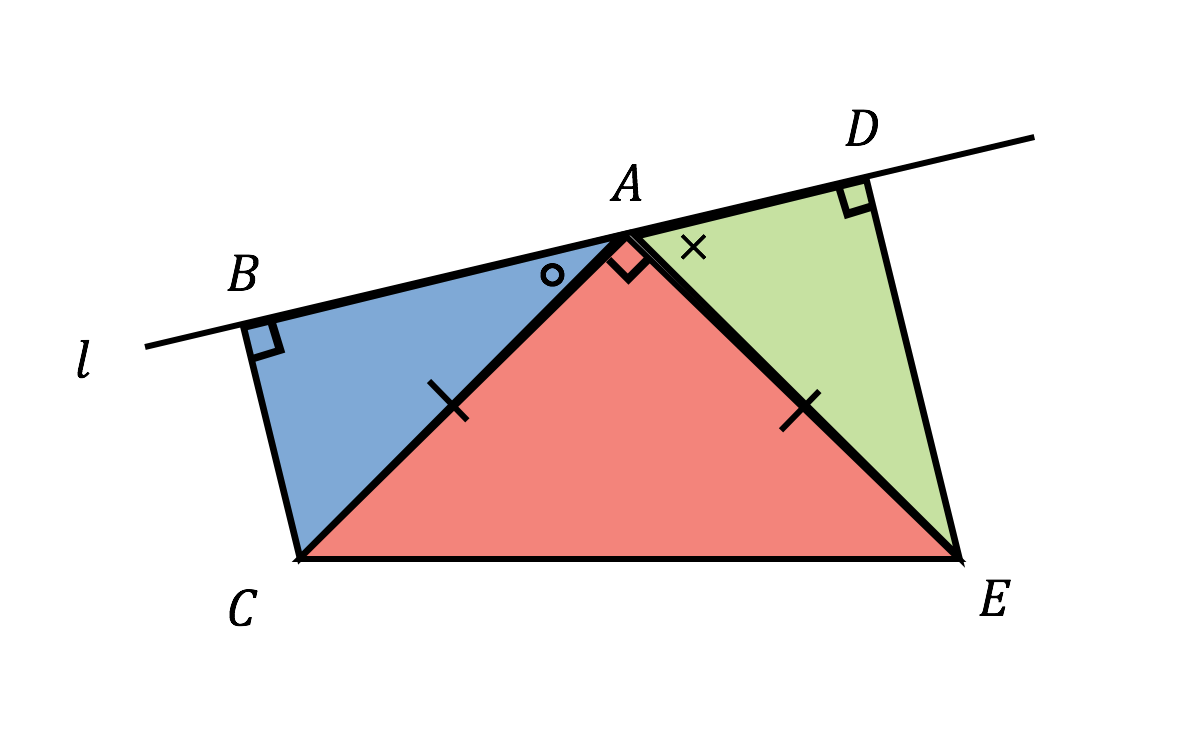



3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ



3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ



Perfume トライアングル 直角二等辺三角形 ある広告人の告白 あるいは愚痴かもね
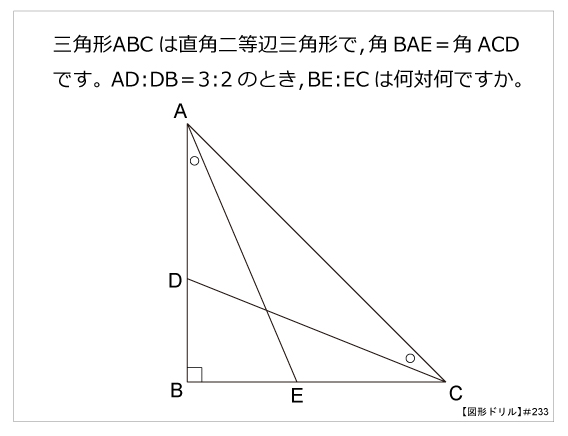



図形ドリル 第233問 直角二等辺の辺の比 算数星人のweb問題集 中学受験算数の問題に挑戦




中学数学 三平方の定理 直角二等辺三角形 オンライン無料塾 ターンナップ




直角二等辺三角形の面積を求める公式は 覚えずに自分でつくろう
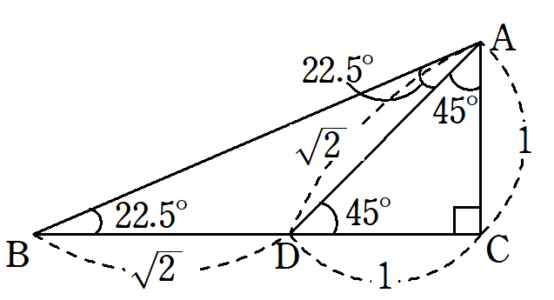



22 5 の三角比 Fukusukeの数学めも




11等边三角形面积公式勾股定理初中数学初二 Youtube
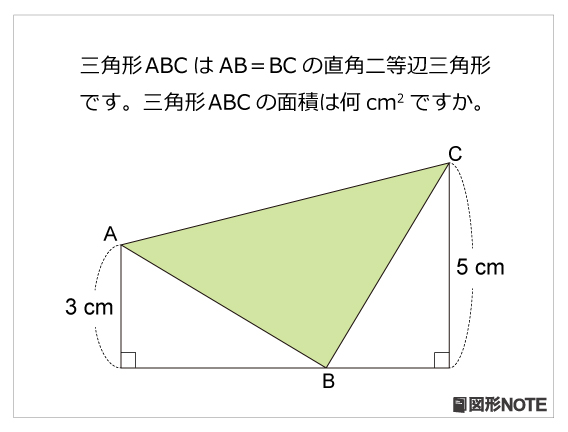



図形noteプレ レベル5 直角二等辺三角形 算数星人のweb問題集 中学受験算数の問題に挑戦
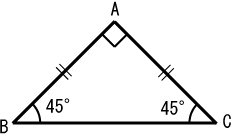



直角二等辺三角形 Wikipedia




โน ตของ 確認 三平方の定理 直角二等辺三角形 ช น Senior Clear




二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比




直角二等辺三角形10枚で正方形 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください




簡単公式 直角二等辺三角形の面積の2つの求め方 Qikeru 学びを楽しくわかりやすく




面積 直角二等辺三角形 小学4年生算数 そらいろ日記 言葉の宝箱




二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比



直角二等辺三角形befの面積は 2006年算数オリンピック ファイナル問題より 算数オリンピック問題に挑戦




30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学




トップ100 正三角形面積小学生 最高のカラーリングのアイデア




簡単公式 直角二等辺三角形の辺の長さの2つの求め方 Qikeru 学びを楽しくわかりやすく




簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比
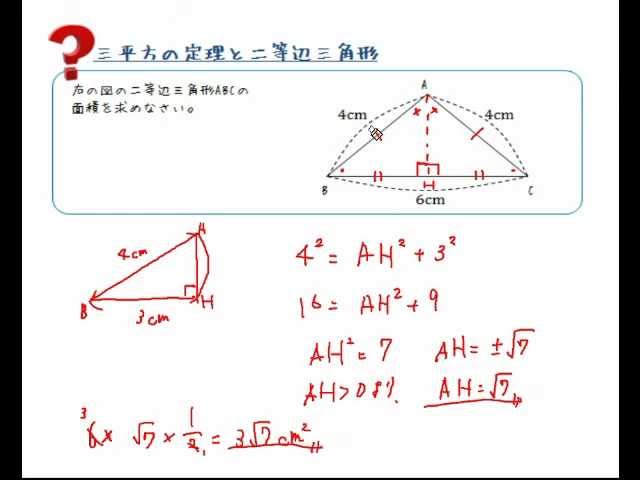



三平方の定理と二等辺三角形 Youtube
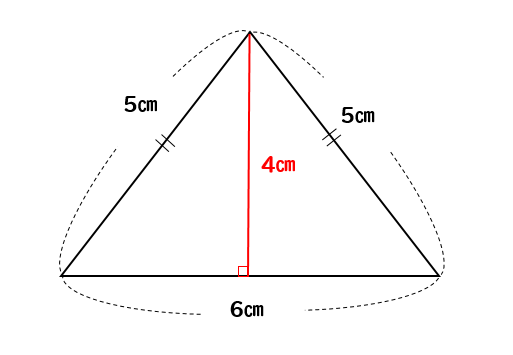



高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ



直角二等辺三角形とは 定義や辺の長さの比 面積の求め方 受験辞典




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ



直角二等辺三角形の辺の長さは 1分でわかる求め方 公式 辺の長さと角度の関係 証明




二等辺三角形 Wikipedia




0405 直角三角形內最大的正方形面積 Youtube




高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ
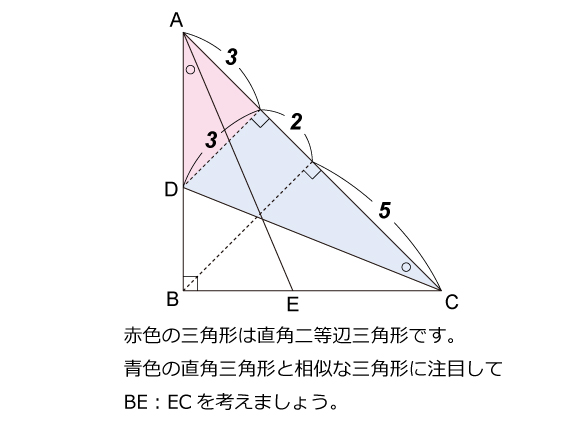



図形ドリル 第233問 直角二等辺の辺の比 算数星人のweb問題集 中学受験算数の問題に挑戦




三角比 30 45 60 もう一度やり直しの算数 数学



直角二等辺三角形の辺の長さは 1分でわかる求め方 公式 辺の長さと角度の関係 証明




30度三角形30 Qmog Fi
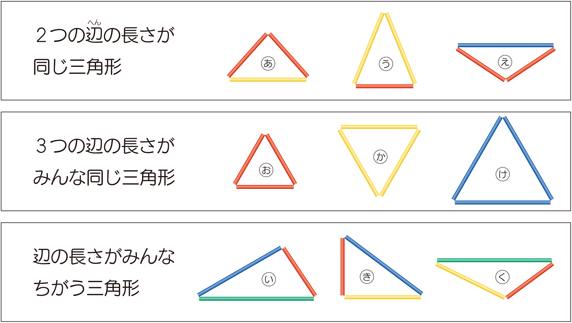



二等辺三角形と正三角形 算数用語集




高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ




高校数学 三角形の形状 正三角形 二等辺三角形 直角三角形 受験の月




トップ100 正三角形面積小学生 最高のカラーリングのアイデア




簡単公式 直角二等辺三角形の面積の2つの求め方 Qikeru 学びを楽しくわかりやすく




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ




簡単公式 直角二等辺三角形の面積の2つの求め方 Qikeru 学びを楽しくわかりやすく




簡単公式 直角二等辺三角形の辺の長さの2つの求め方 Qikeru 学びを楽しくわかりやすく




無料印刷可能直角二等辺三角形 比率 最高のぬりえ
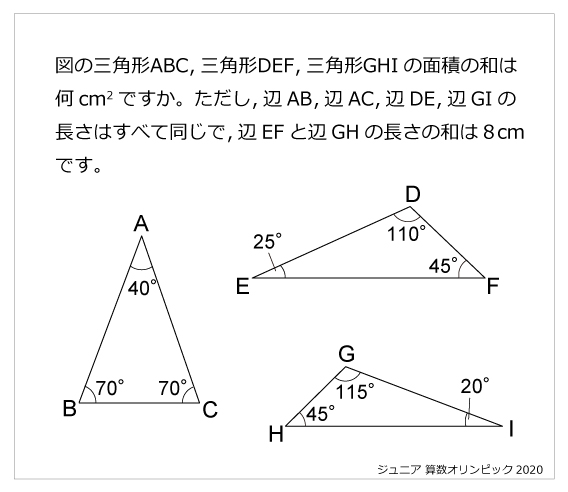



直角二等辺三角形 算数星人のweb問題集 中学受験算数の問題に挑戦



働きアリ 数学科



0 件のコメント:
コメントを投稿