・この公式を理解するためには、三角形の内角の和は180°という公式を使います。 このn角形の内角の和の公式は、中学生で習う内容です。 ただ、実は 小学生でも多角形の内角の和について習っている ので、その復習にもなっている公式です。1日15分で一生使える中学数学の全公式 文字式、円の面積から平方根、中点連結定理まで、中学3年間の数学で学ぶ公式・定理・決まり事が効率よく理解できる便利な1冊。 1項目、見開き2ページ完結で読みやすい構成です。 著者 (肩書) 監修:小西豊文 丸暗記するのではなく、多角形の性質をしっかり確認して公式を使うようにしていきましょう。 多角形の内角の和六角形の内角の和を求める場合上のように4つの三角形に分けられるので、三角形の内角の和は180°だから六角形の内角の和は 180×4=7° となる。

N邊形內角和定理 Youtube
多角形 内角 公式
多角形 内角 公式-形」と呼び,本研究では特徴的な双曲多角形の公式や性質について考えた.「対辺の長さ が等しい双曲4角形の性質」命題33 や,「等辺直角n 角形(全ての辺の長さが等しく,全 ての内角が直角であるn 角形) の一意性」命題35 を示すために,ランバートの4角形(3 面積公式 多角形の面積は、頂点の位置ベクトルから 外積 を用いて計算することができる。 多角形の頂点を反時計回りに並べて、それらの位置ベクトルを という式になる。 ただし、 とする。 この式を使うと凹多角形でも問題なく計算できるが、自己




如何计算角度 8 步骤 包含图片
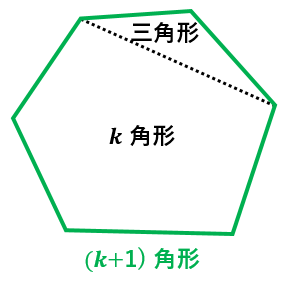
多角形の内部の任意の2点を結ぶ線分がその多角形の内部に含まれる ような多角形を凸多角形(convex polygon)という. この定義では対象となる2点対が無限に存在するので,計算不可能. 性質1:多角形Pが凸多角形であるための必要十分条件は,Pのすべての 多角形の内角の和 = 線を引いて現れた三角形の数 × 180 これをもっと簡単な公式にします。 上の図をると、三角形の数は多角形の角の数より2つ少ないことがわかります。 球面の面積は分割された多角形の面積の和であるので冒頭の公式より, S R 2 = \dfrac{S}{R^2}= R 2 S = 全ての内角の和 − ∑ n (n − 2) π c n\displaystyle\sum_{n} (n2)\pi c_n − n ∑ (n − 2) π c n 一つの頂点の周りの角度は球面でも 2 π 2\pi 2 π なので,全ての内角の和は 2
頂点の数「n」でわると正多角形の1つの内角の大きさになるよ。 180× (n2)/n どの内角も同じ大きさだからね! まとめ:正多角形の内角は「総和」を「頂点の数」でわれ! 正多角形の内角の公式は、 180°×(n2)/n だったね。 ようは、多角形の内角の和の公式 \(\color{red}{180^{\circ}\times (n2)}\) を覚えているのなら、当然ですが正多角形にも使えるので \(\hspace{10pt}180^{\circ}\times (92)\\ =1260^{\circ}\) でも、もちろん良いです。 または外角の和がいつも\(\,360°\,\)であることから、 正九角形の外角の1つは 数学・算数 多角形の内角の求め方が分かりません。 教科書には「180°×(n-2)」とあるのですが、この式の意味がよく分かりません。 「(n-2)」とはどこから来ているのでしょうか? 宜しくお 質問No
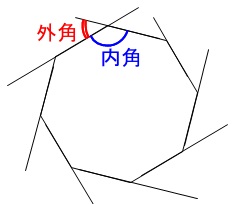
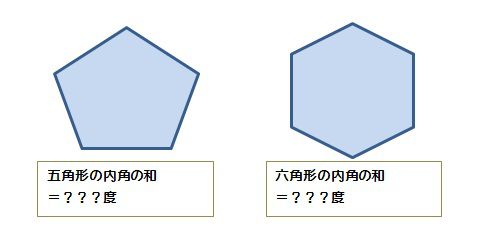
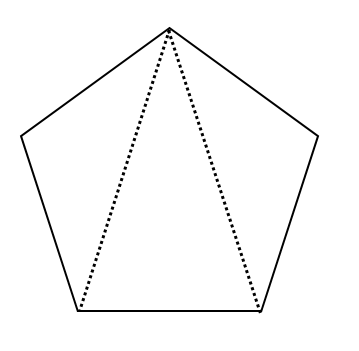
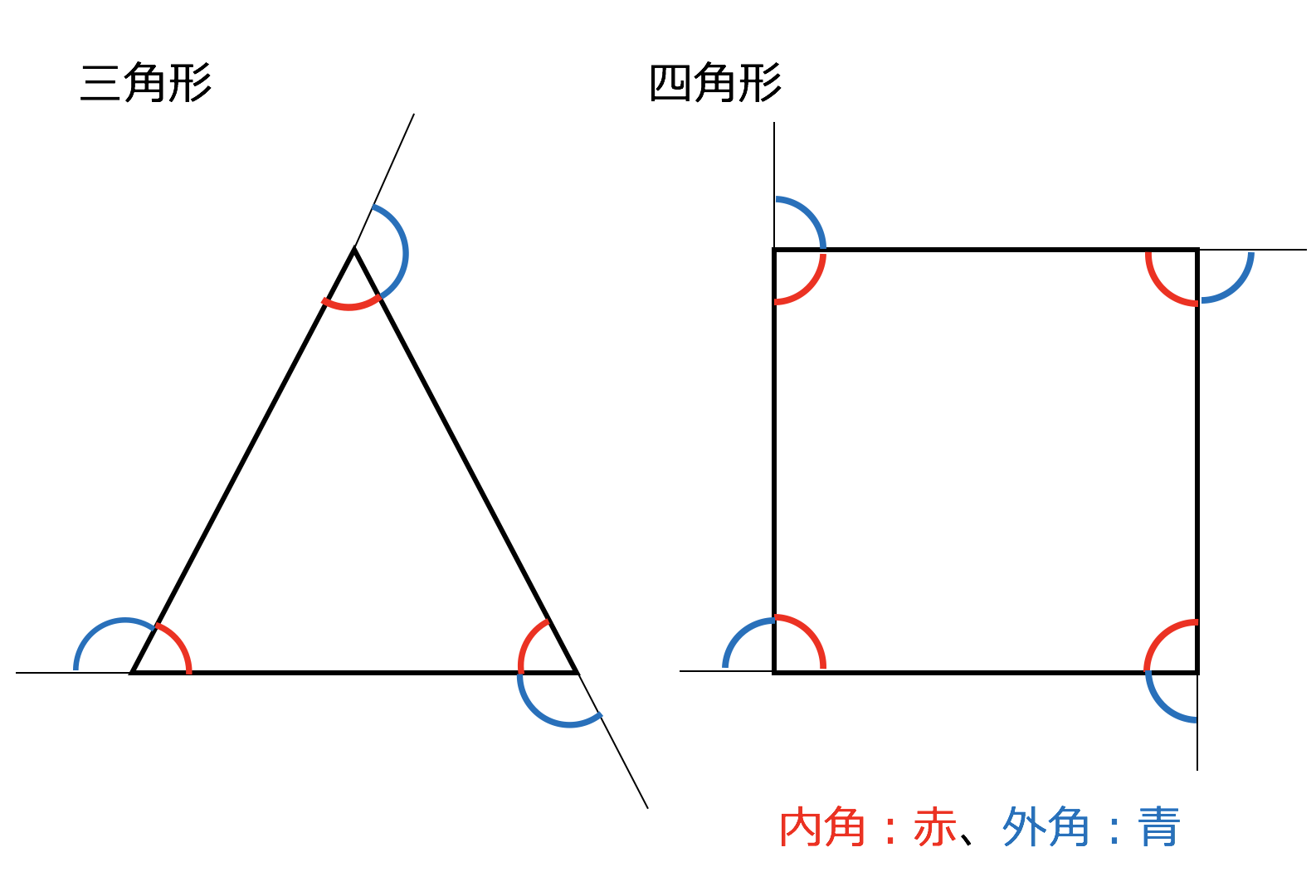
多角形の内角の和 ここでは四角形以上の"多角形の内角の和"について考えてみましょう。 ではさっそく、 下に五角形と六角形の図があるので、それぞれの内角の和を考えてみましょう。 考え方は四角形の 算数では様々な公式を覚えます。 しかしその公式の意味を知っている方は多くないと思います。 本ホームページでは公式の意味や公式の導き方を図を使用角というのは、直線や線分が交差した点と、その両端の線で挟まれた部分のことを言います。 多角形はどのように区別がされているかというと、この角の数によってされています。 左から「三角形」「四角形」「五角形」です。 また、図形の内側の角を 内角 といい、それから延長した辺と1辺がつくる角を 外角 といいます。 この2つの角度を足すと 180° になり 正多角形モード /1/6 プログラミング教育 ビスケットの新バージョンをリリースしました(kindleは現在審査中です).このバージョン,細かい修正が入っているんですが,一番目につきやすいのが正多角形モードを追加した点でしょうか. Flashの



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典
三角形の内角の和 (角度を全部たしたもの)が 180° になるのは知っているよね。では、角が多い、多角形の内角の和はどうなるんだろう。 そこで、今日のポイントだよ。 公式の意味 重要なのは,この公式を丸々覚えることではなく, 三角形の内角の三角関数の和は積に,積は和に変換できる という事実を覚えておき,その場で導出できるようにしておくことです。 ちなみに, a b c = π abc=\pi a b c = π でなくて a b c = 2 π abc=2\pi a b c = 2 π のときなどクリーム色の三角形の内角 \(2\) つの和は、 緑色の三角形の内角 \(2\) つの和と等しいです。 よって、はじめの \(5\) つの角の和は、 下の図の赤い三角形の内角の和と等しいので、\(180°\) と求まります。 例題2 下の図で、印をつけた角の大きさの和を求め



多边形内角和定理 快懂百科



五边形内角和是多少 天奇教育
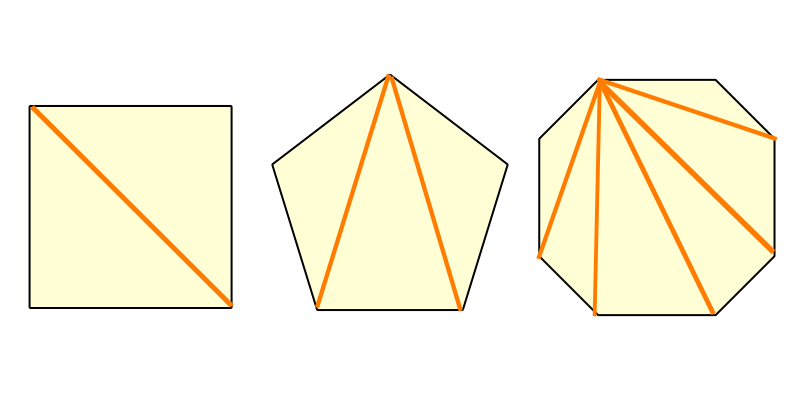
AFJ の内角の和より180° x y A B C D E a d b b c Hd Fe G H I J 外側の五角形から付け足した三角 形5つ分を引き,内角の五角形をた すと, 180°×(5-2)-180°×5 +180°×(5-2)=180° e G d B e H B C D D E a b c d e F G I J J四角形なら180°が2つだから360° 五角形なら180°が3つだから540° 六角形なら180°が4つだから7° ・・・ って、線を引いたら三角形ができるので、180°がいくつあるかでその多角形の内角の和を求めることができます 多角形の内角の和、外角を利用した問題です。基本公式をしっかり理解して解いていきましょう。 基本公式 *多角形の外角の和は360°になる 公式を丸暗記するのではなく、公式の導き方を教科書で確認し、自分でも証明できるようにしておいてください。




10多边形的内角和进阶平行四边形初中数学初二 Youtube



初中数学多边形内角和 掌握一个公式 学会内外角结合求解边数
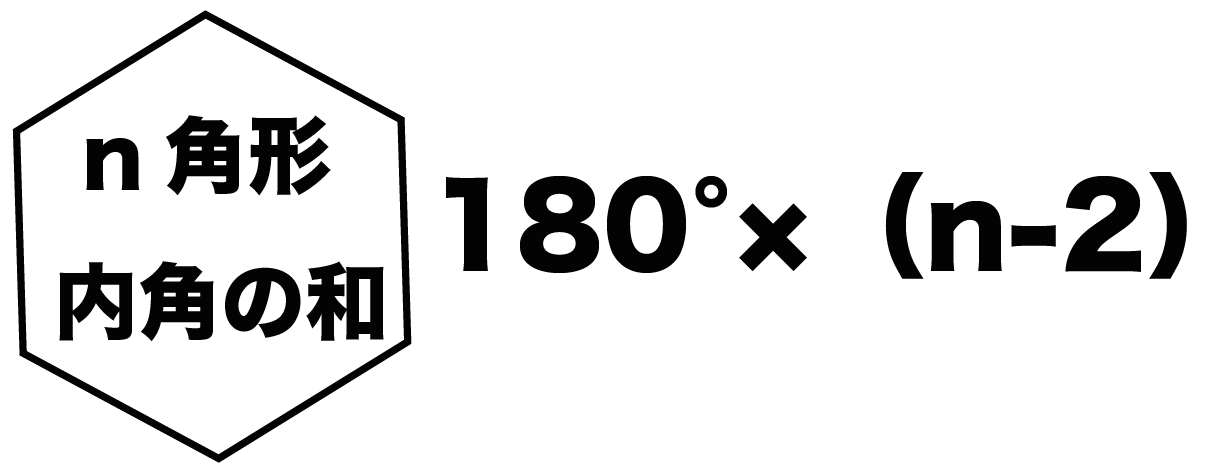
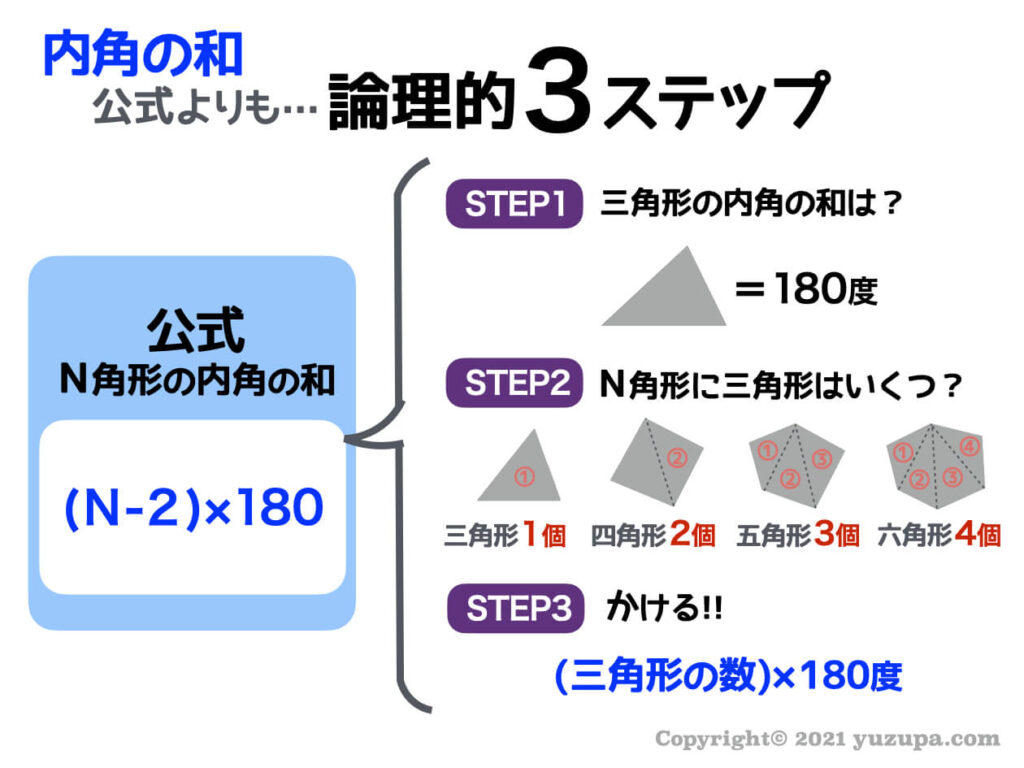
N N 角形の内角の和は、180 × (N − 2)° 180 × (N − 2) °内角の和は 180°×2=360° となった。 五角形の場合も同じように考えると、 3 つの三角形がで きるので、内角の和は 180°×3=540° 六角形の内角の和は、 180°×4=7° n 角形の場合を考えると、一つの頂点から対角線を引い 外角・内角の和、面積、対角線の本数の公式と求め方 21年2月19日 この記事では、「多角形」の種々の公式(外角の和・内角の和、面積、対角線の本数など)やその求め方をわかりやすく解説していきます。 また計算問題の解き方もわかりやすく解説して




多角形の内角の和の公式と外角の和を利用した角度の求め方



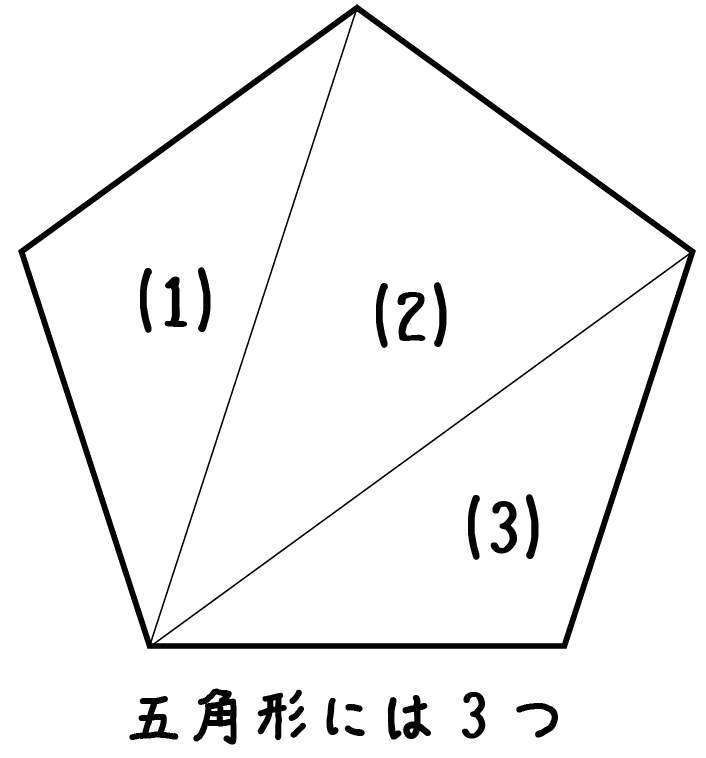
五边形的内角和是多少公式 经验
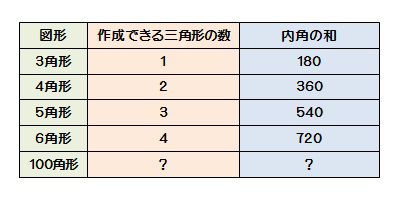
・星形六角形の頂角の和は,ほとんどの生徒が求めている。 <発表された生徒の解き方> (4) レポート作成の課題を与える。 1) 頂角の和が180度になる星形多角形を調べよう。 2) 星形偶数多角形の性N角形の内角の和=180×(n-2) この公式を忘れてしまったらどうしたらよいでしょうか? 多角形の内角の和は求められないでしょうか? そんなことはありません。 忘れてしまった場合は、前項で使用したこんな表を自分で作成してみましょう。 三角形 多角形の内角の和を求める公式 多角形の内角の総和は、上記のように補助線を引いて三角形がいくつできるかで知ることができます。 また、上記のことから、以下の公式を導くことができます。 多角形の内角の和 = 180° × ( 頂点の数 - 2 )
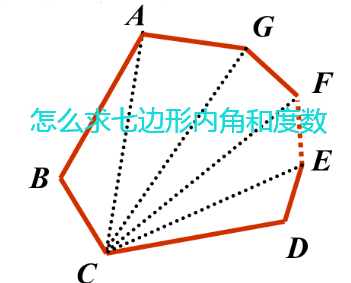



怎么求多边形内角和与外角和的度数怎么求七边形的内角和度数



多边形一个内角的公式 西瓜视频搜索
まず、多角形の内角の和は $$\LARGE{180 \times (n2)}$$ で求めることができましたね。 正三角形の内角の和であれば $$\LARGE{180 \times (32)=180°}$$ ★ 多角形の5つのポイント ①外角の和=つねに360度 ④内角の和=180×( -2) -2だったか -3だったか忘れやすいので 五角形を例 に公式を思いだせるようにしておきましょう。 ★公式順番に考えて星形多角形 を作図し、頂角の和を求 めてみよう。どんなこと に気がつきますか。 ,。。。 54。。寒。 ⑥ 本時のまとめと次時の予告 頂角の和が何度であるか、予想(実測)させる 多角形の内角の和の性質についてもふれる



多边形内角和是多少度 初三网



N边形的内角和是多少 西瓜视频搜索
(内角) (外角) =180° (外角) =180°− (内角) 多角形の内角の和と外角の和の公式 N角形の内角の和: 180°×(N−2)180°×(N−2) 多角形の外角の和: 360°360° 難しく感じるかもしれませんが、内角の和は三角形が180°。 そこから角が増えるごとに内角の和も180°ずつ増えていきますよーということです。 それに対して、外角の和は角が増えても変わらず常に360°です。正多角形のひとつの内角: 正 n n 角形のひとつの内角の大きさは, 180°× n−2 n 180 ° × n − 2 n



数学中多边形的内角和公式是什么 初三网



正多边形内角和 正多边形内角和公式 尚书坊
多角形の外角の和は、 いつでも360° 。角の数に関係ないんだ。 公式を利用して、例題をいっしょに解いてみよう。



正多边形内角和多边形内角和公式推导方法 尚书坊




多角形の内角の和 は何度なのか を説明します おかわりドリル
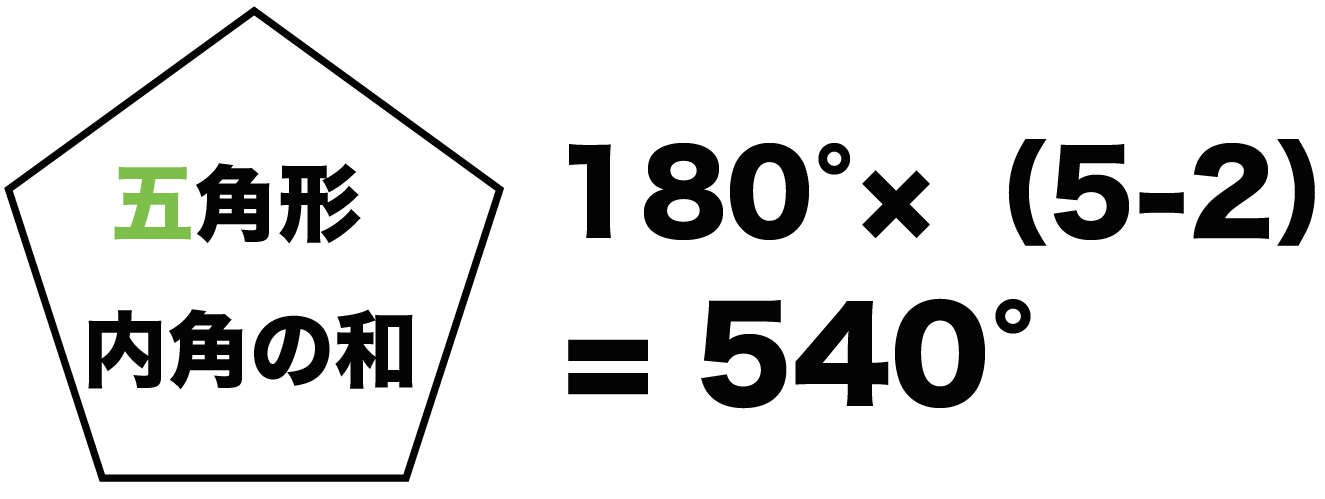



中2数学 多角形の内角の和が3秒でわかる公式 Qikeru 学びを楽しくわかりやすく



正多边形内角和公式 高中数学 七千寻文化 追梦传奇人生



初三数学多边形内角和公式知识点总结 初三网



正多边形内角和公式及定义 高三网



N边形的内角和计算公式 西瓜视频搜索




计算内角之和 提示 21



一球面多边形及其内角和公式 人教版高中选修3 3数学电子课本 数九网




中2数学 多角形の内角 外角 図形の合同 ひっそりと物理や数学を解説する



多边形内角和公式 多边形内角和公式 多边形 内角 和 公式 早旭阅读网



已知 多边形的每一个外角都等于40度 则这个多边形是 边形 共有 条对角线 其内角和为 度 初中一年级 数学试题 多边形的内角 和和外角和考点 多边形考点 好技网




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun




人教初中数学八上word全册打包教案 第4套人教初中数学八上11 3 多边形及其内角和 教学设计 小库档文库




计算内角之和 提示 21




多边形内角和公式正多边形内角和公式及定义 学习问题 100教育家长学院




内角和外角 维基百科 自由的百科全书



1




N邊形內角和定理 Youtube




つくばサイエンスエッジ18 文京学院大学女子高校 みらいぶ 高校生サイト




多边形的内角和 公开课下载 Word模板 爱问共享资料




中考重头戏 多边形到圆 极致到完美 每日头条



N边形的内角和计算公式 西瓜视频搜索



多边形内角和定理 西瓜视频搜索



中2数学 多角形の内角の和が3秒でわかる公式 Qikeru 学びを楽しくわかりやすく



正多边形内角和多边形内角和公式推导方法 尚书坊



N边形的内角和公式 初三网




3分で分かる 多角形の内角の和の求め方 公式の証明などをわかりやすく 合格サプリ




多角形とは 内角の和の求め方を簡単に解説 高校生向け受験応援メディア 受験のミカタ



多边形内角和公式的推导 慧诚教育 学习视频教程 腾讯课堂




多边形内角和公式多边形内角和公式推导 学习问题 100教育家长学院



多角形の内角の和の公式と外角の和を利用した角度の求め方




多角形の内角の和 算数の公式覚えてますか



求多边形内角和公式多边形内角和公式王计算多边形内角和是06度 老师告诉他
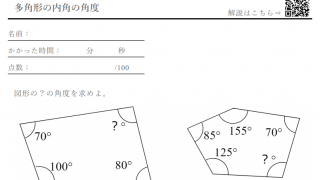



多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun




多角形の内角の和の公式を3通りの方法で証明する 具体例で学ぶ数学
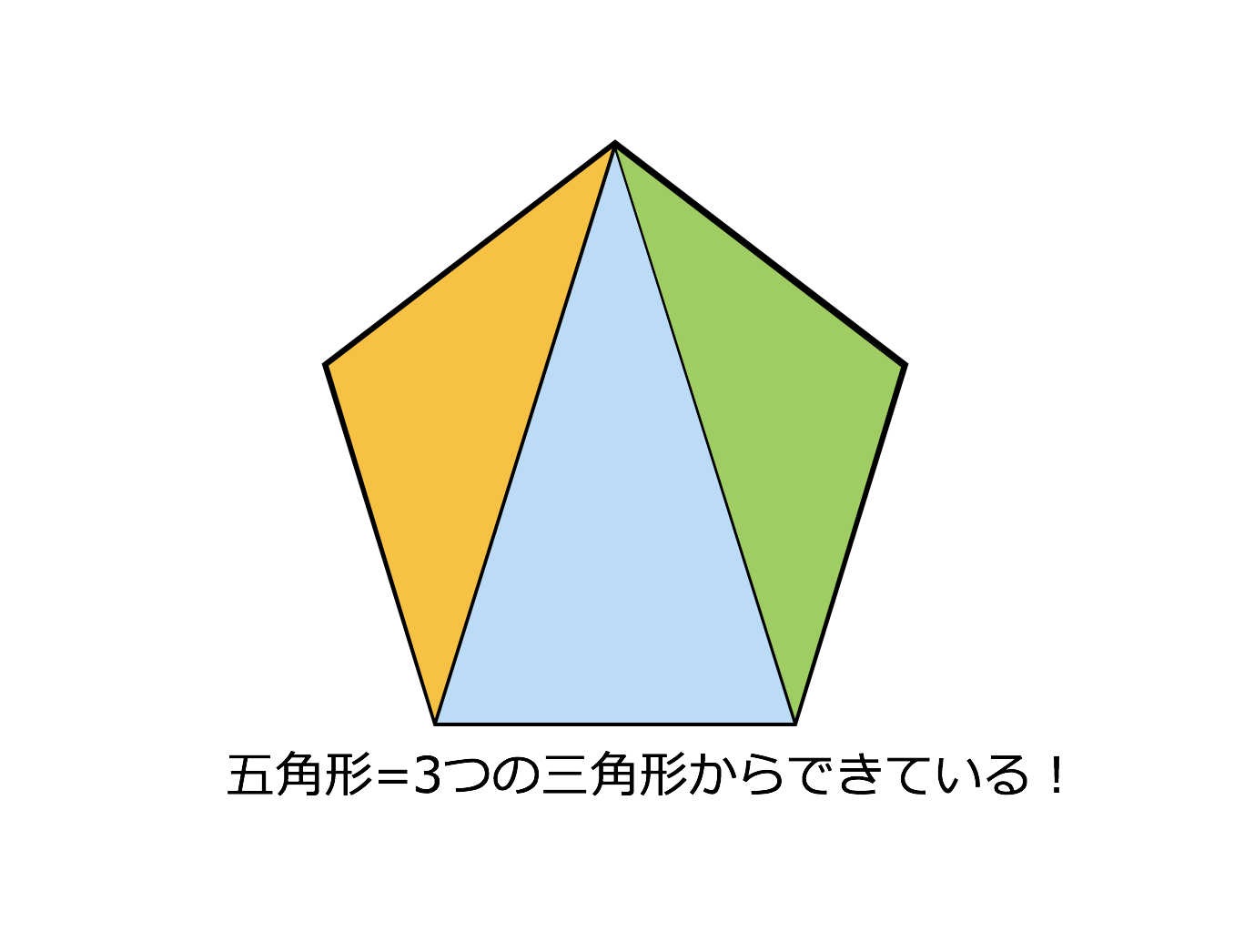



3分で分かる 多角形の内角の和の求め方 公式の証明などをわかりやすく 合格サプリ
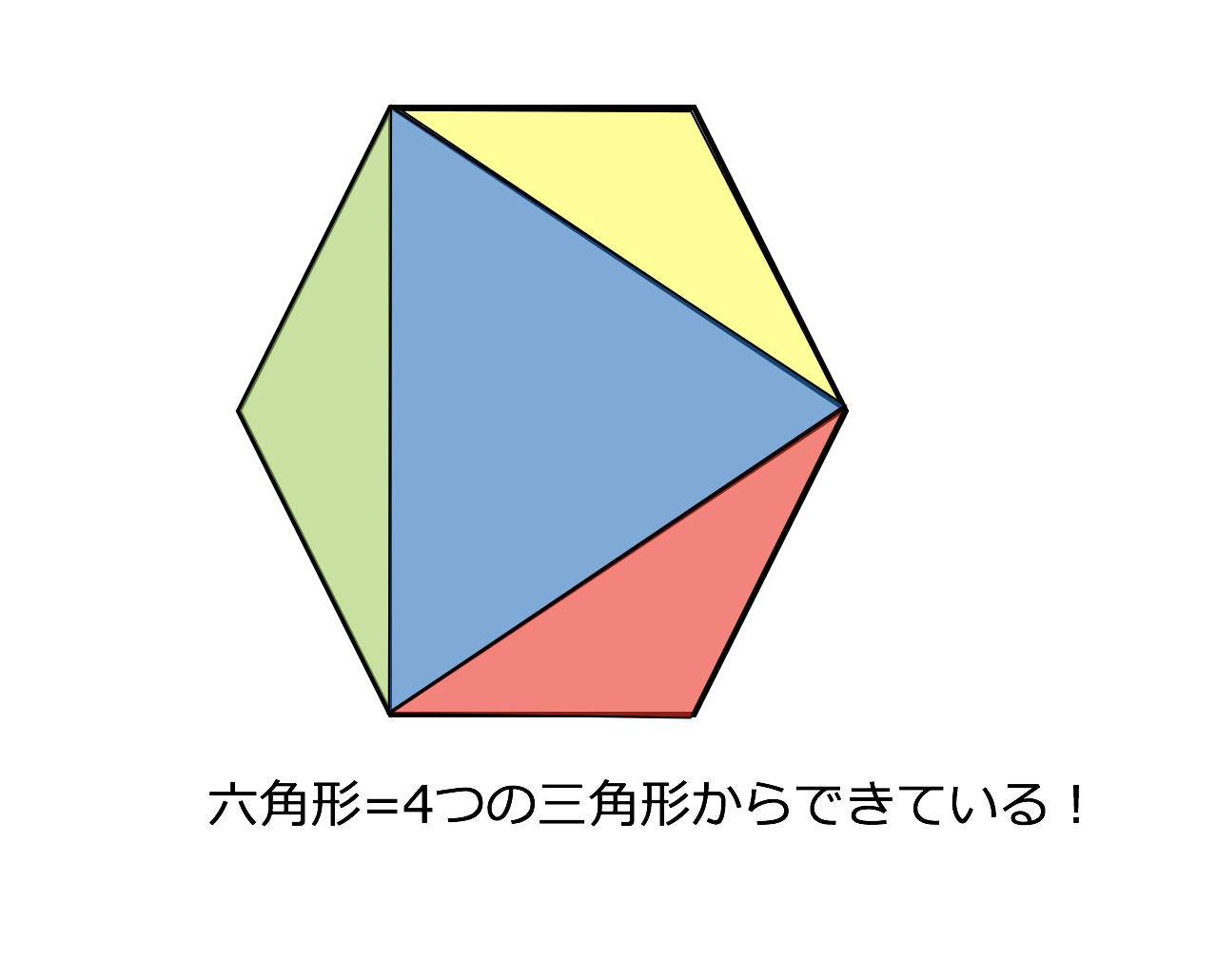



3分で分かる 多角形の内角の和の求め方 公式の証明などをわかりやすく 合格サプリ




如何计算角度 8 步骤 包含图片
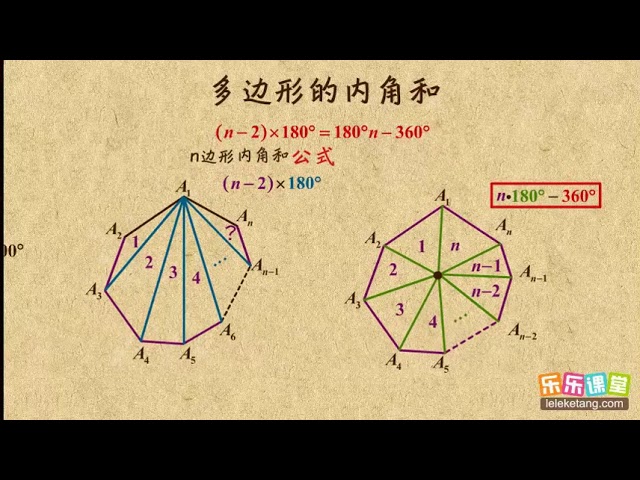



08多边形的内角和平行四边形初中数学初二 Youtube



多边形一个内角怎么求 初三网



五边形的内角和是多少 多边形内角和怎么求 多边形的内角和公式 秦学教育



正多边形内角和多边形内角和公式推导方法 尚书坊



正多边形边数公式 多边形内角和度数公式 尚书坊




多角形の内角の和 外角の和の公式 数学fun




计算内角之和 建议 June 21



初三数学多边形内角和公式知识点总结 初三网



多角形の内角の和 算数の公式覚えてますか




五边形内角和 五边形内角和是多少度



N边形的内角和计算公式 西瓜视频搜索



中2数学 多角形の内角の和が3秒でわかる公式 Qikeru 学びを楽しくわかりやすく



多角形の内角の和 算数の公式覚えてますか



多边形内角和公式




多角形の内角の和の公式を3通りの方法で証明する 具体例で学ぶ数学




正八角形的内角 八角形的内角是多少度 三人行教育网 Www 3rxing Org




内角和外角 维基百科 自由的百科全书




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun



五边形的内角和是多少 多边形内角和怎么求 多边形的内角和公式 秦学教育



多边形内角和公式是什么 初三网




多角形の内角の和の求め方をイチから解説するぞ 中学数学 理科の学習まとめサイト




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun



多角形の内角の和の公式を3通りの方法で証明する 具体例で学ぶ数学



求几边形的公式 西瓜视频搜索



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典



正多边形边数公式 多边形内角和度数公式 尚书坊



内角是什么 初三网




3分でわかる 多角形の外角の和の求め方 Qikeru 学びを楽しくわかりやすく




多角形の内角の和 算数の公式覚えてますか



正多边形内角和是多少 多边形内角和公式推导过程



正五边形的内角和是 时习社区



3分で分かる 多角形の内角の和の求め方 公式の証明などをわかりやすく 合格サプリ



N边形的内角和计算公式 西瓜视频搜索




3分でわかる 多角形の外角の和の求め方 Qikeru 学びを楽しくわかりやすく




五边形内角和和外角和 五边形的内角和的度数是多少 三人行教育网 Www 3rxing Org



多角形内角 Article



中学受験 多角形の内角の和 公式を忘れなくする論理的3ステップ かるび勉強部屋




七边形内角和是多少 巧解多边形的内角和 星火网校



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典



多角形の内角の和 簡単に計算できる電卓サイト



正多边形内角和 正多边形内角和公式 尚书坊




3分でわかる 多角形の外角の和の求め方 Qikeru 学びを楽しくわかりやすく
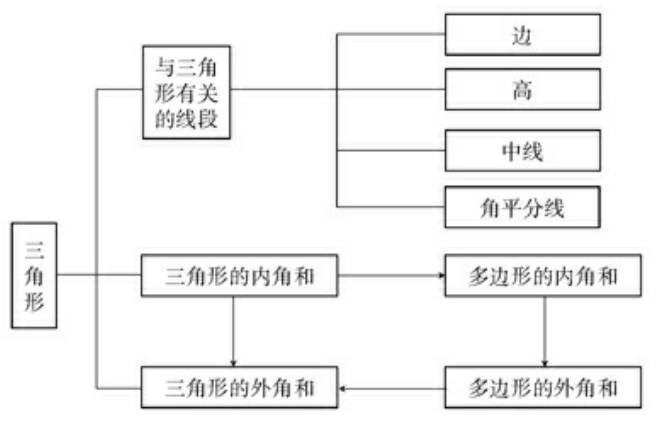



寒假预习 人教版七年级数学下册知识点及公式 三角形 内角



多边形的内角和公式怎么算 初三网




多角形の内角の和 外角の和の公式 数学fun



教师资格面试数学试讲 多边形的内角和 试讲稿 答辩 安徽山香教育




已知两边求角度公式 初中数学多边形内角和 掌握一个公式 学会内外角结合求解边数 不要芝麻酱的博客 程序员宅基地 程序员宅基地



0 件のコメント:
コメントを投稿